微信红包背后的赌博游戏

序

今天坐车的时候，看到司机的微信在玩一个叫「红包接龙」的游戏，让我提起了兴趣。游戏的规则很简单：群里有 100 个人，首先群主发一个 100 元的红包，然后大家去抢。抢到最多钱的那个人（手气最佳）必须再发一个 100 元的红包，依次类推。乍一听，如果每个人都遵守规矩，那么这就是一个零和游戏。但仔细品品感觉并不那么简单。在这个情况下，是不是资产很容易两极分化，然后其中一些人破产呢？又或者，存不存在一种玩法，使得可以必胜呢？于是我想来好好讨论一下这个问题。

随机算法

要想探讨这个游戏，首先我们需要知道微信红包是怎么进行随机算法的。根据这个知乎回答，答主给出了一个微信红包的算法。由于具体的算法是一个黑盒，那么我们就先建立在这个算法下进行好了，也就是：

每个人随机从 0.01 和剩余平均值两倍之间取一个值，最后一个人拿走剩余全部。

我写了一个小 Ruby 脚本来实现这个功能：

require 'descriptive_statistics'
require 'securerandom'

class RedEnvelope
  def initialize(money, size)
    @size = size
    @money = money
  end

  def draw
    raise 'Empty Envelope' if @size < 1

    if @size == 1
      @size -= 1
      return @money
    end

    max = @money / @size * 2
    aquired = SecureRandom.random_number(max - 1) + 1

    @size -= 1
    @money -= aquired
    aquired
  end

  def empty?
    @size == 0
  end
end

class User
  attr_reader :name, :money

  def initialize(name, money)
    @name = name
    @money = money
  end

  def generate(money, size)
    raise "#{@name} Go Bankrupt" if money > @money
    @money -= money
    RedEnvelope.new(money, size)
  end

  def fetch(envelope)
    fetched = envelope.draw
    @money += fetched
    fetched
  end
end

class Game
  attr_accessor :users
  def initialize(bet, users)
    @bet = bet
    @users = users
    @round = 0
  end

  def play(user)
    @round += 1
    order = @users.shuffle
    largest_amount = 0
    largest_user = nil
    envelope = user.generate(@bet, @users.size)
    order.each do |user|
      amount = user.fetch(envelope)
      if amount > largest_amount
        largest_amount = amount
        largest_user = user
      end
    end
    print "Round #{@round}: "
    puts @users.map { |u| u.money / 100.0 }.standard_deviation
    largest_user
  end
end

标准差与破产探索

我们先假设有 10 个玩家，每个人有 5000 元开局，每一把玩 200 元好了。

users = []
10.times do |i|
  users << User.new("User #{i}", 5_000_00)
end

game = Game.new(200_00, users)

user = users.first
loop do
  user = game.play(user)
end

进行了一次模拟，在游戏进行到第 2399 轮时，2 号玩家破产。玩家间余额的标准差随游戏轮数的关系如下：

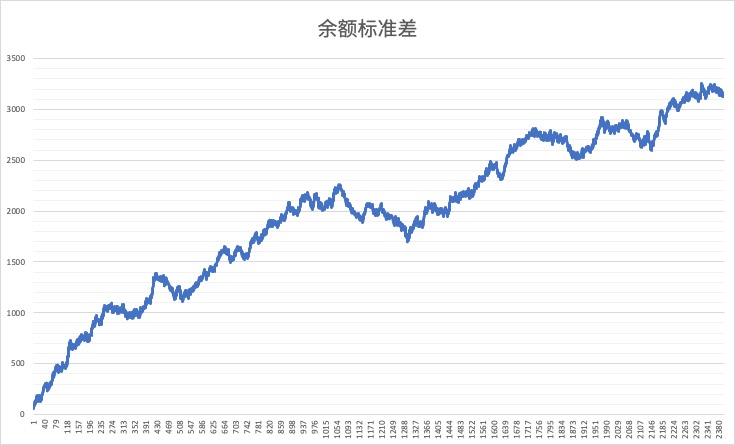
std-env

多进行几次模拟，修改初始金额或每次的赌资，情况几乎不变。也就是随着游戏轮数的进行，玩家间余额的标准差（贫富差距）在变得越来越大，直到某一玩家破产，游戏结束。

这一结论是显然的，因为实际上这个游戏是一个典型的「无偏随机游走」问题，标准差与时间成正比。随着游戏进行，必然一些人变得极度有钱，而越来越多人会破产。

随机算法的不随机之处

但财富不单单是聚集的问题，如果我们仔细回头看这个随机算法，就会发现它是有规律的。

虽然均值一样，但是越早抽到红包，方差越小，越不可能遇到需要发红包的情况。越后抽越容易出现手气最佳，从而产生负收益的情况。在均值一致的情况下，只要减少发红包的次数就行了。于是，庄家如果有机器辅助的话，就可以把自己的期望变为正数。

但是，这时我就产生了一个疑问：「如果同时也有其它机器人一起参与抢单呢？」

我于是问了问司机，这群有人用抢红包工具吗？司机非常自信地告诉我：「不可能。群主会先收取押金，如果你被发现作弊，会直接把你踢出群。」

原来如此，原来只要把连着几把第一个抽的直接踢出群没收押金即可。

完美。

结论

十赌九输，

赌博前请先学数学。

CodeRemixer

序

随机算法

标准差与破产探索

随机算法的不随机之处

结论