用 Ruby 学习基本乐理（二）：音程

在上一篇文章里，我们认识了音高。这相当于学会了怎么数数。学完数数的小朋友就要学习加减法了，而音高之间的加减法就叫音程。说到「音程」，最类似的日常词语是「路程」。路程是两点间的距离，音程也是两个音高之间的距离。描述音程有两种方法，一种简单的，一种常用的。

音数

简单的方法就是我们执行数学上的减法运算，也就是所谓「半音数差」。比如 C 和 D 之间隔了 2 个半音。

我们把上次的代码稍稍改一下就可以计算音数差了。既然是音数就是个减法运算，我们就可以通过在 Ruby 中实现一个减法方法，从而可以实现 Tone 类之间的减法运算。

class Tone
  STANDARD_TUNING = 440.0
  attr_reader :frequency, :name, :offset

  def initialize(name)
    @name = name
    @offset = parse_name(name)
    @frequency = frequency_by_offset(@offset)
  end

  def parse_name(name)
    raise AugumentError unless name.match?(/^[CDEFGAB][#,b]*\d$/)
    tone = name[0]
    sharps = name[1...-1]
    range = name[-1].to_i
    
    # Calculate offset
    major_scale = [-9, -7, -5, -4, -2, 0, 2]
    offset = major_scale['CDEFGAB'.index(tone)] + (range - 4) * 12 # Offset without sharps or flats
    
    sharps.chars.each do |c|
      c == '#' ? offset += 1 : offset -= 1
    end

    offset
  end
  
  def frequency_by_offset(offset)
    STANDARD_TUNING * (2.0 ** (1.0 / 12)) ** offset
  end

  def harmonic_series(max=Tone.new('B9').frequency)
    tones = []
    (2..).each do |n|
      break if @frequency * n > max
      tones << Tone.by_frequency(@frequency * n)
    end
    tones.uniq { |t| t.name }
  end

  def -(tone)
    raise TypeError unless tone.is_a?(Tone)
    @offset - tone.offset
  end

  class << self
    ALL_TONES = (0..9).map {|range| ['C', 'C#', 'D', 'D#', 'E', 'F', 'F#', 'G', 'G#', 'A', 'A#', 'B'].map {|name| "#{name}#{range}"}}.flatten.map { |name| Tone.new(name) }

    def by_frequency(freq)
      errs = ALL_TONES.map {|x| (x.frequency - freq).abs }
      ALL_TONES[errs.rindex(errs.min)]
    end
  end
end

p Tone.new('C3') - Tone.new('D3') # => -2

我们 C3 比 D3 低了 2 个半音，完美。

音级

另一种对音程的描述是基于音级的。在上篇文章我们说到过

音高到音名的关系是一对多的，D、C## 可以表示同一个音高（取决于作曲家的具体需求）。

这是因为在乐理中，音高是在某一个音阶（音高的集合）上的概念。当要在具体音符上使用升降记号时，说明是要使用音阶外音。而音阶外音就需要标注是从音阶中哪个音变化过去的。这就是为什么像是 C# 和 Db 在乐理中是两个不同的音。这一点在五线谱上实际上是特别清晰的，但是很多流行音乐或者电子音乐的制作流程已经完全是基于 midi 乐器的。而 midi 乐器只关心实际的频率，通常都是在钢琴卷帘上进行创作的，是完全不区分 C# 与 Db 的，这也是很多流行音乐创作者容易犯的乐理错误。

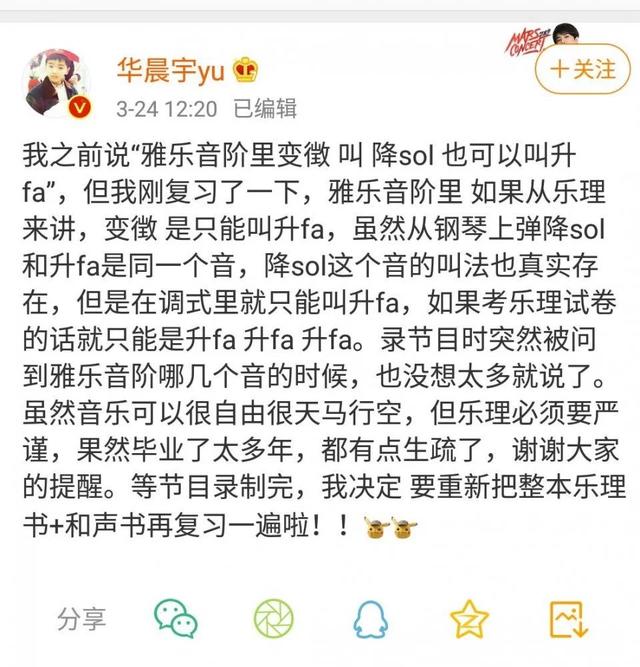
F-Sharp Mistakes Example

（这下理解流行乐坛乐理小王子怎么在节目里讲乐理被真音乐学院副教授给骂了吧。）

但是我们刚刚的基于音数的音程计算方法，完全不能体现出这样的特性。于是我们应该在描述音的距离的时候，要基于音阶上的音，同时也要能给出不少于音数的信息量。描述音阶上的音我们就要引入音级的概念。

音级	C	D	E	F	G	A	B
C	1	2	3	4	5	6	7
D	2	1	2	3	4	5	6
E	3	2	1	2	3	4	5
F	4	3	2	1	2	3	4
G	5	4	3	2	1	2	3
A	6	5	4	3	2	1	2
B	7	6	5	4	3	2	1

音级是描述音名与音名之间的距离关系，单位是度，这一关系完全忽略升降号。然而比较奇怪的是，相同音是 1 度音，而不是 0 度。换句话说，纯一度是这个音级加法群的单位元，而不是大家熟悉的 0。

def interval_number(tone)
  raise TypeError unless tone.is_a?(Tone)
  if self - tone > 0
    'CDEFGAB'.index(@name[0]) - 'CDEFGAB'.index(tone.name[0]) + (@name[-1].to_i - tone.name[-1].to_i) * 7 + 1
  else
    'CDEFGAB'.index(tone.name[0]) - 'CDEFGAB'.index(@name[0]) + (tone.name[-1].to_i - @name[-1].to_i) * 7 + 1
  end
end

p Tone.new('C3').interval_number(Tone.new('D3')) # => 2
p Tone.new('C3').interval_number(Tone.new('G2')) # => 4
p Tone.new('C3').interval_number(Tone.new('C1')) # => 15

型态

对于音级的修饰叫「型态」，乐理上有 5 种基本型态：大、小、纯（完全）、增、减。分别用 M, m, P, A, d。其中 1 4 5 8 度用的是增、纯、减这三个词，而 2 3 6 7 度用的是大、小、增、减。在 C 大调上 C D E F G A B C1 与 C 的关系分别是纯一度大二度大三度纯四度纯五度大六度大七度纯八度。比大音程小一个半音的叫小音程。比小音程或纯音程小一个半音的叫减音程，而比大音程或纯音程大一个半音的叫增音程。然后更大更小的再前面用倍字修饰。

所以理论上 C 和 D#### 之间的音程是「倍倍倍增二度」，而频率完全相同的 C 和 F# 则是「增四度」。

def interval_type(tone)
  raise TypeError unless tone.is_a?(Tone)
  semitones = (self - tone).abs % 12
  number = (interval_number(tone) - 1) % 7 # Eighth's type is equal to union's.
  default_type_semitones = [0, 2, 4, 5, 7, 9, 11]
  default_types = %w(P M M P P M M)
  delta = semitones - default_type_semitones[number]
  current_type = default_types[number]

  until delta == 0
    if delta > 0 and (current_type == 'P' or current_type == 'M')
      delta -= 1
      current_type = 'A'
    elsif delta > 0
      delta -= 1
      current_type = "A#{current_type}"
    elsif delta < 0 and (current_type == 'P' or current_type == 'm')
      delta += 1
      current_type = "d"
    else
      delta += 1
      current_type = "d#{current_type}"
    end
  end

  current_type
end

p Tone.new('C3').interval_type(Tone.new('D3')) # => "M"
p Tone.new('C3').interval_type(Tone.new('G2')) # => "P"
p Tone.new('C3').interval_type(Tone.new('C1')) # => "P"

总结

最后我们结合一下这两者：

def interval(tone)
  "#{interval_type(tone)}#{interval_number(tone)}"
end

p Tone.new('C3').interval(Tone.new('D3')) # => "M2"
p Tone.new('C3').interval(Tone.new('G2')) # => "P4"
p Tone.new('C3').interval(Tone.new('C1')) # => "P15"
p Tone.new('C3').interval(Tone.new('D####3')) # => "AAAA2"

至此，我们用 Ruby 处理了乐理中与音程有关的常见问题。让我们对 Ruby 和乐理的熟练程度都进一步提升了。接下来，我会介绍如何进一步用 Ruby 来处理和弦。

CodeRemixer

音数

音级

型态

总结