女朋友问你「我是不是世界上最好看的女人?」怎么办
如果你女朋友问你「我是不是世界上最好看的女人?」
错误回答:
- 是的。(除非你见过世界上所有女人)
- 不是。(会没命)
- 我不知道。(太虚伪,你女朋友真的比电视上的明星都好看吗?)
正确回答:
- 我觉得美貌不是一个全序关系 (total order) 或偏序关系 (partially ordered)。
- 不小于三个标准差吧。
「好看」背后的抽象代数
什么是全序集?
关于什么是「最好看」,我们需要理解一下序。也就是先定义一下什么是「好看」。如果让我们把好看直接量化成一个数字可能太难了。但是我们通常是可以比较两个人之间谁比较好看的问题的。于是我们可以假设一个二元关系(Binary relation),比如 $\geq$,使得对于一个所有女人的集合 $S$ 中存在某两个元素 $a$ 和 $b$,如果 $a$ 比 $b$ 好看,我们就记作 $a \geq b$。
全序集有三个性质:
- 传递性。即如果 $a \geq b$,且 $b \geq c$,那么蕴含 $a \geq c$。
- 反对称性。即如果 $a \geq b$ 且 $b \geq a$,那么 $a = b$。
- 完全性。即 $a \geq b$ 与 $b \geq a$ 必有一个成立。
比如我们的整数就是一个全序集,如果整数的个数是有限个的,那么就会存在一个「最大」的数。好在地球上人类的数量是有限的,那么如果「好看」是一个全序集,那么会存在「最好看」的人(可能不唯一)。
为什么美貌不太可能是个全序关系?
如果我们遇到 $a \geq b, b \geq c, c \geq a $ 同时成立。如果根据反对称性和传递性,我们易证三者是一样好看的。但在自然语言中,好看的关系通常是严格的,即 $a \gt b, b \gt c, c \gt a $ 。这样三者的序形成了一个环,而不是链,所以美貌不太可能是个全序关系。
不是全序一定没有最好看吗?
在非全序关系中,「最好看」虽然不一定会存在,但也可能会存在。一种常见的可能存在的序是偏序。即不需要满足「完成性」,只需要完成自反性,即 $\forall a \in S, a \geq a$。一个典型的例子就是子集集合包含排序。
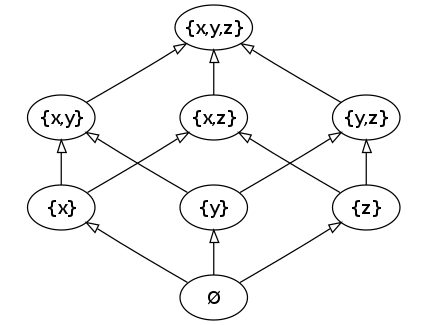
偏序集的特点是可能存在某两者无法比较,也就是可能存在数个无法比较的「最好看」,于是我们无法判断出这些「最好看」里谁是真正的「最」。
不过美貌的序关系可能也不是偏序,因为我们刚刚遇到了「环」的问题。偏序集同样是无法成环的,其应该是一个有向无环图。一旦成环的位置在「最好看」里,我们也会遇到类似于偏序集无法选出「最好看」的问题。
于是你可以把这个问题抛回给你女朋友,「怎么证明这个世界上『最好看』是存在的」?
如果我们假设美貌是全序关系
如何假设美貌的分布
即使我们抛开对于「好看」序关系的讨论,假设「好看」是可以被量化的。但是由于我们无法接触到世界上所有的女性,我们只能给出一个估计。而这个估计必须先假设一个统计学分布。考虑到大部分人的长相是平凡的,我觉得我们可以假设是「高斯分布 (Gaussian distribution, 常态分布, 正态分布)」的。所以我们可以给出一个对标准差下限的估计来描述女友的好看程度。
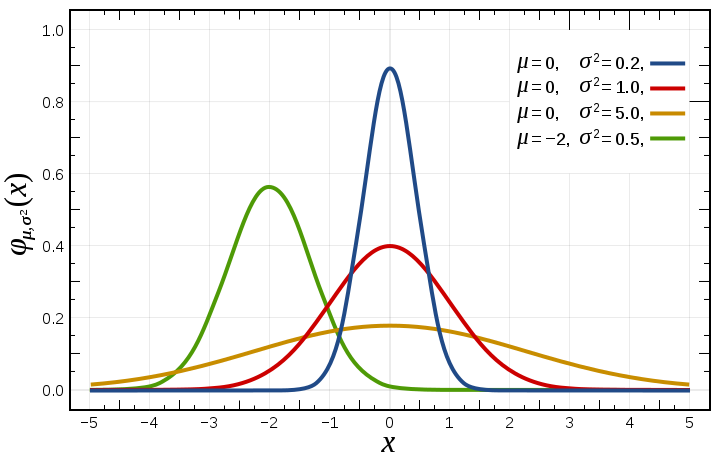
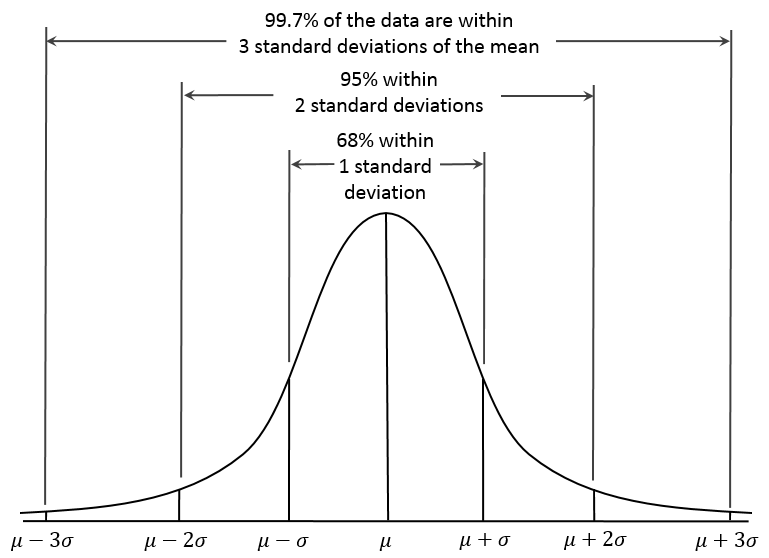
三个标准差的美貌有多好看?
我们在样例答案中描述的「不小于三个标准差吧」即估计女友的好看程度能大于 99.73% 的女性,这应该是一个很高的称赞了,毕竟我们会接触过的女性可能也很难超过 $10^4$ 这个数量级。
「我和迪丽热巴谁好看?」
使用这一基于正态分布的理论,可以有效扩展到另一个送命题上,即「我和迪丽热巴谁好看?」。
你可以反问「你觉得迪丽热巴有 4 个 σ 吗?」。
这个问题不最大的难点在于,很难精确实质上估计 4 个 σ 的可信度。就算是 IQ 测试通常也无法估计到这个级别以上。这个分布基本上是本科线上被清华录取的概率,可能和一大堆明星中出一个超大爆款的概率差不多在一个数量级上。
我倾向认为迪丽热巴是有的,不过你女朋友如果不是一线艺人且觉得自己也有的话,恐怕是要相当有自信了。
不是数学没有用,是你不会用
虽然很多人都认为学数学是没有用的,会一点加减乘除就行。但是在这个例子中,我们通过学习抽象代数和统计学巧妙化解了女友问出的「送命题」。
虽然我没有女朋友,但是数学理论只要自洽应该就可以。这套自洽的体系对于「真空中的球形女朋友」应该适用。不过我也不做保证,要是你用标准答案失败了,建议你去换个数学更好的女友比较好。
大家都学会了吗?
