浮点数如何导致了 4.92000008 级地震?
刚收到一个地震速报,说美国发生了一场 M4.92000008 级地震。这个数字实在太过于微妙,我们很少见到精确到小数点后那么多位的地震级数。News Digest 网站迅速删除了这篇报道,并且补上了一篇 M4.9 级的报道。
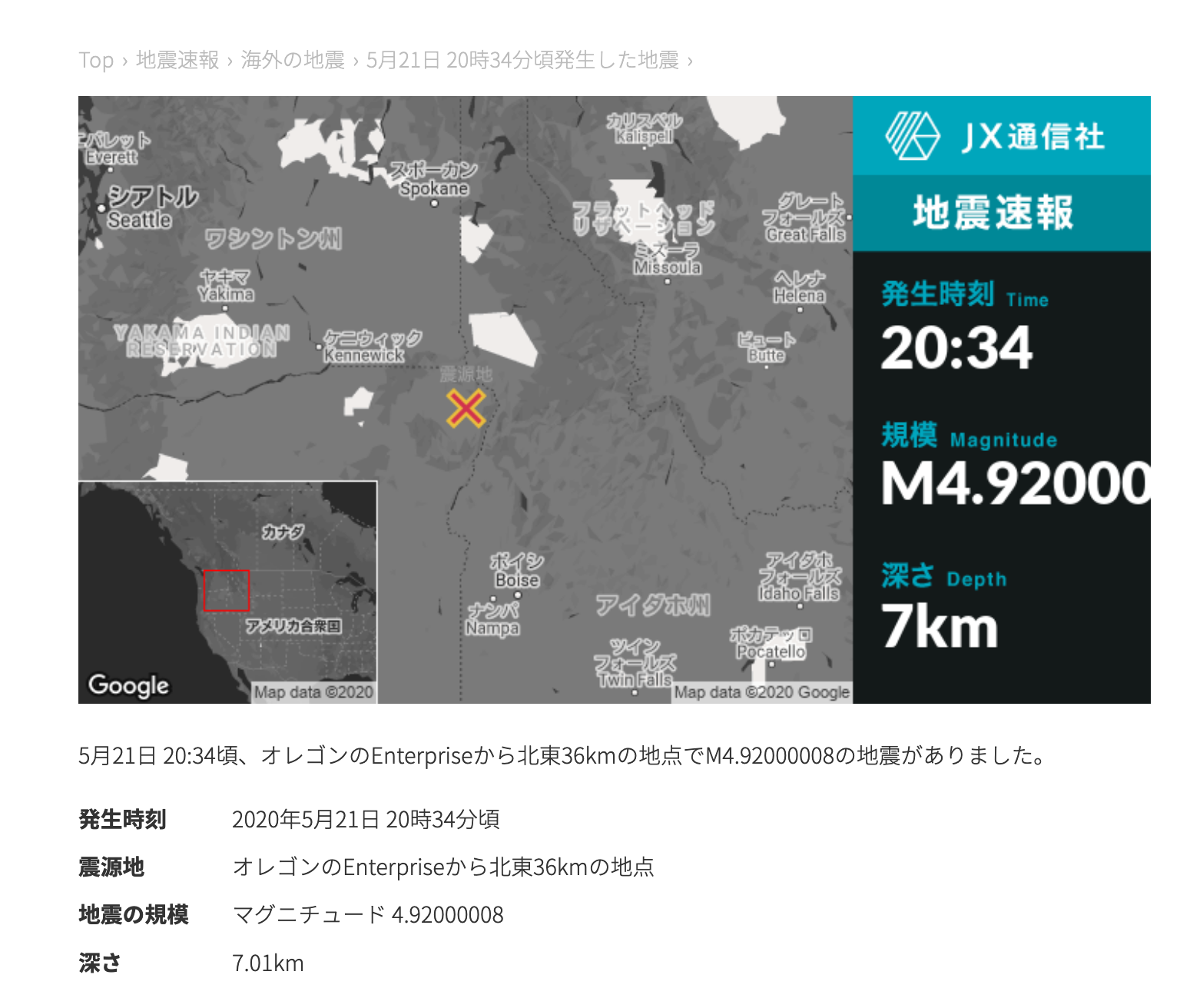
然而,这么奇怪的地震级数是怎么发生的?
计算机如何表达小数?
要想理解这个问题,我们还是要从计算机表达数字的方法开始说起。如果要在计算机里表达小数,有两个主流方法,定点数和浮点数。
定点数很好理解,对于一个二进制,我们人为规定其某几位是整数部分,而另外某几位是小数部分。例如我们对于下面一个 8 位无符号的数字,定义第四位是分割点。
| $2^3$ | $2^2$ | $2^1$ | $2^0$ | $2^{-1}$ | $2^{-2}$ | $2^{-3}$ | $2^{-4}$ |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
那么这么一个 10011001 就代表十进制的 9.5625。
我们很容易看出,这个数字里能表达的最大的数字是 11111111,即十进制的 15.9375。
定点数的点点在哪里是非常关键的,如果点在最后,那么其实就只是整数,不能表达小数,但是能表达的数字最大;如果点在太前面,那么虽然表达小数的能力很强,但是却不能表达大数。
然而浮点数小数点的位置是浮动的。我们可以根据数据的情况来调整浮点的位置。实际的浮点数还有规约和特殊值的问题,不过我们可以暂且简化一下这个问题。
比如对于下面的一个八位数字。前四位表示指数即 $2^{8-x}$ 次方,后面部分表示小数即 $1+y$。
| x | y | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
我们可以知道,这里 $x = 5, y = 0.5625$,所以结果是 $(1+0.5625) \times 2^{8-5} = 12.5$。这个数字能表达的最大值是
| x | y | ||||||
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
结果是 $(1+0.9375) \times 2^8 = 496$,比定点数大很多。浮点数在大数字时能显示的位数更多,而在小数时能显示更高的精度,这在我们不确定精度的时候是一个很好的选择。
浮点数与定点数之争
这两个方法谁更好,在历史上有过一段时间的争斗。
一个失败的定点数的应用就是在 Sony PlayStation 游戏机上。Sony PS 的处理器不支持浮点数计算,只支持定点数计算。Sony PS 的定点数是一个 16.16 定点数,即使用一个 32 位的数据结构,将前 16 位表示整数,而后 16 位表示小数。包括 PS 3D 坐标的顶点变换运算也不得不使用这套定点数系统。在表达小数字时计算就会出现精度不足的情况,这使得 PlayStation 在渲染 3D 图形时经常会出现模型抖动的问题。
在一般的计算中你通常会需要浮点数,因为当数字小的时候我们更关心精度,而大了之后我们更希望能存储大数。所以在大多数编程语言中,都会提供浮点数作为最常用的小数数据类型。不过定点数在一些场合仍在使用,比如说在一些 NPU(Neural-network Processing Unit)处理器中,会使用定点数来消除浮点数导致的精度抖动。而大多数神经网络中都会由于归一化的存在而很好控制住数据的范围,不会出现大数的情况。
回到 4.92000008 级地震
我们通常所说的浮点数,指 IEEE 754。即由电机电子工程师学会 (IEEE) 规范的一套浮点数算法。对于一个 32 位(单精度)浮点数,第 1 位表示正负号,后面 8 位表示指数(即 2 的多少次方),然后接下来 23 位是偏正值,并且还对规约、零、无穷、NaN 进行了特别的定义,是目前最常用的浮点数。
让我们来看看如何用 IEEE 754 浮点数表达 4.92 级地震。
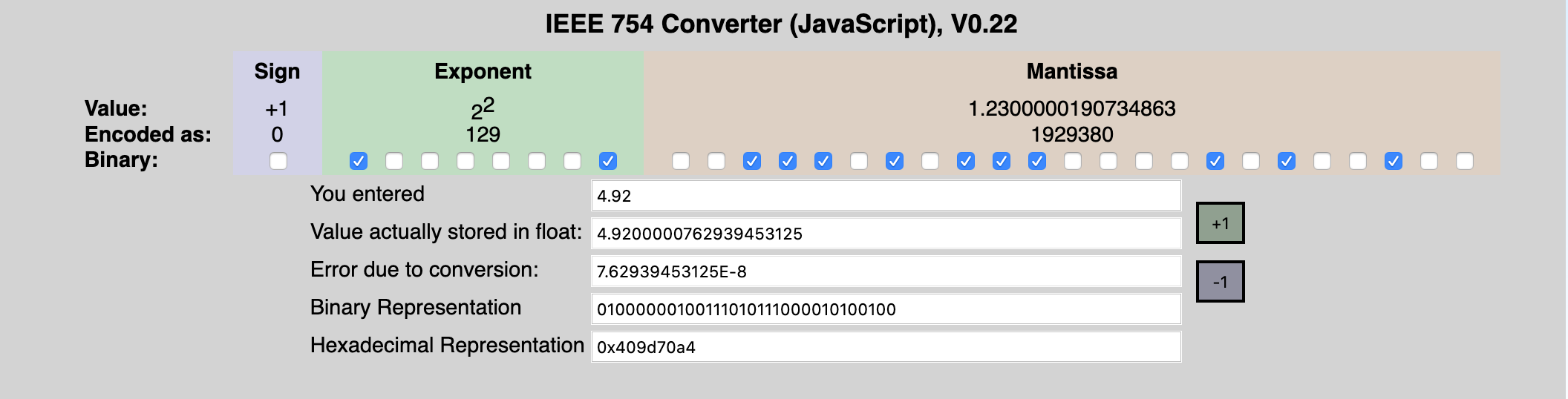
我们可以看到,表达成二进制后产生了一个 0.0000000762939453125 的误差,也就是变成了 4.9200000762939453125,如果我们精确到小数点后 8 位,就变成了 4.92000008。
啊,原来不是测了个那么精确的地震,是浮点数弄出了一点误差,而发布的时候忘记精确到小数点后 2 位了啊。
举一反三
那么聪明的你,能告诉我,为什么在很多语言里 0.1 + 0.2 等于 0.30000000000000004 吗?
