用 Ruby 实现飞机自动驾驶仪

krpc 是一个砍巴拉太空计划（Kerbel Space Program）中的插件。可以通过 RPC 来控制游戏。同时有第三方的 Ruby 客户端：krpc-rb。和真实飞机不同的是，在砍巴拉游戏中驾驶飞机是非常痛苦的，在没有插件辅助的情况下，你看不到具体的 GPS 坐标，很多时候看到的都是和飞机驾驶无关的轨道参数，而一些关键的控制参数缺很难获取。同时游戏中也没有自动驾驶仪。特别在航天飞机降落的控制非常难，虽然手动降落不会太有问题，游戏对于重着陆的容忍度很高，但是要控制飞机飞往机场的过程漫长而痛苦。于是我们试试看利用 krpc 来实现正常商用飞机都有的自动驾驶仪的功能。

PID 控制

PID 是自动化控制中最基础也是最常用的控制算法。

我们假设我们要控制汽车油门使得汽车的速度达到某个我们预想中的速度。最直接的想法就是基于距离目标速度的大小来调整油门。也就是说越接近目标速度，我们油门踩得越轻。

但这会产生一个问题，由于我们控制的是给油，油门到加速度控制存在一个延迟，使得我们放开油门后的几毫秒内可能速度还会上升；而当我们看到速度超过放开油门的量越来越大，随着车速越来越快，我们受到的空气阻力实际在增加，车速又会很快下降，而无法与加速度达到平衡，这种情况下我们就会在目标速度附近来回震荡。根据我们按比例控制的激进程度，振幅可能有所变化，最坏情况下我们会震动幅度越来越大，使得系统完全失控。

解决这个问题最直接的方法是引入一个积分项，不单单根据目前速度的误差，也要根据当前加速度的积分，也就是速度来判断。速度越大可能我们需要的油门也要更大一些。

最后我们实际控制还会遇到扰动的问题，我们可能还要根据过去一段时间内误差变化幅度来调节油门大小，比如遇到一个晃动速度快速下降，我们就要快速补一下油门来弥补这个误差。这意味着我们还要引入一个微分项。把这三个结合起来，我们可以得到公式： \(u(t) = K_pe(t) + K_i\int_0^te(\tau)d\tau+K_d\frac{d}{dt}e(t)\) 形成一个通用的 P（比例）I（积分）D（微分）控制器。不过虽然说是通用，这每一项前面的系数比例要想调好也是不容易的。我们会用这个控制器来分别控制飞机的节流阀、滚转和俯仰。

用 Ruby 实现出来是这样的：

class PIDController
  def initialize(kp, ki, kd, clip_min=0.0, clip_max=1.0)
    @prev_err = 0.0
    @integral = 0.0
    @kp = kp
    @ki = ki
    @kd = kd
    @clip_min = clip_min
    @clip_max = clip_max

    @last_frame = 0.0
  end

  def trigger(goal, measured)
    trigger_err(goal - measured)
  end

  def trigger_err(err)
    current_frame = Time.now.to_f
    dt = current_frame - @last_frame
    if dt > 1.0
      @last_frame = current_frame
      return 0.0
    end

    @integral = @integral + err * dt

    @integral = @clip_min if @integral < @clip_min
    @integral = @clip_max if @integral > @clip_max

    d = (err - @prev_err) / dt
    res = @kp * err + @ki * @integral + @kd * d
    @prev_err = err
    @last_frame = current_frame

    return @clip_min if res < @clip_min
    return @clip_max if res > @clip_max
    res
  end
end

实际实现和公式有一些细微差异。积分项不能比可以控制的最大值更大，也不能比最小值更小。否则当误差和控制不在一个数量级的时候，往往会出现很难控制或者反应迟钝的问题。

起飞控制

起飞控制比较简单，在打开 SAS 保持稳定的情况下，我们只需要控制系统加速到抬轮速度，然后将飞机抬头到俯仰 10 度，收起起落架。最后爬升到给定的高度。

class TakeoffProcess
  def initialize(vessel, vr, velocity, height)
    @vessel = vessel
    @control = vessel.control

    @vr = vr
    @velocity = velocity
    @height = height

    @throttle_controller = PIDController.new(0.1, 0.01, 0.2)
    @pitch_controller = PIDController.new(0.05, 0.05, 0.1, -1.0, 1.0)
  end

  def run
    @control.brakes = false
    @control.sas = true
    loop do
      orbit = @vessel.flight(@vessel.orbit.body.reference_frame)
      surface = @vessel.flight(@vessel.surface_reference_frame)
      break unless orbit.speed < @vr
      throttle = @throttle_controller.trigger(@velocity, orbit.speed)
      @control.throttle = throttle
    end

    # Rotate
    puts "Rotate, Gear Up!"
    @control.gear = false

    loop do
      orbit = @vessel.flight(@vessel.orbit.body.reference_frame)
      surface = @vessel.flight(@vessel.surface_reference_frame)
      break unless orbit.mean_altitude < @height - 100
      throttle = @throttle_controller.trigger(@velocity, orbit.speed)
      @control.throttle = throttle

      pitch = @pitch_controller.trigger(10, surface.pitch)
      @control.pitch = pitch
    end

    puts "Takeoff Process Finished."
  end
end

比较麻烦的地方是 ksp 有一个 reference_frame 的概念，很多参数需要的是相对于 reference_frame 参数的概念。比如当你需要速度的时候，有可能获得轨道速度，也可能得到的是地面速度。再比如俯仰，如果是相对于轨道的俯仰，那么理论上始终应该是在 0 附近，因为轨道会随着俯仰变化而变化。所以计算的时候要小心。

方向角计算

起飞后一般飞机自动驾驶仪一个最重要的功能就是根据预先在飞行电脑上设定好的飞行路线来飞行了。路点一般有几个关键参数：高度、速度、经纬度。高度和速度的写法和我们起飞的时候差不多。但转向就比较复杂。

我们首先需要确定的是，飞机要转几度才能转到目标点，也就是计算方位角。我们先来考虑，如果这个地球是一个平面，经纬度是 x 和 y 轴上的坐标，方向角应当怎么算呢？其实我们可以很容易得到方向向量： \((x, y) = (x_b-x_a, y_b-y_a)\) 那么方向角（自正北作为 0 度的顺时针角度）就是 \(tan(\theta)=\frac{x_b-x_a}{y_b-y_a}\) \(\theta = atan(\frac{x_b-x_a}{y_b-y_a})\) 然而在球面上计算这个问题要复杂一些，本质上我们需要知道大圆上任意两点的距离，我们需要用到球面三角学中重要的半正矢公式（Harversine Formula）。

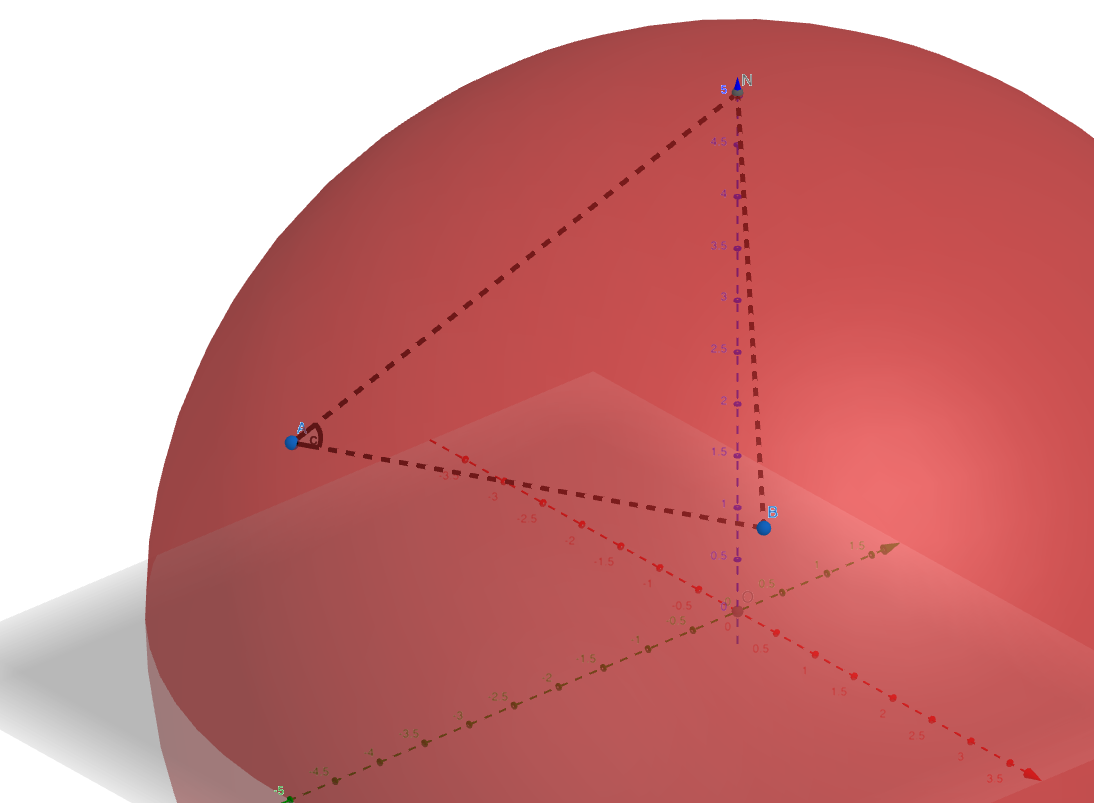
根据半正矢定理，我们有： \(hav(c) = hav(a-b)+sin(a)sin(b)hav(C)\) 其中： \(hav(\theta)=sin^2\frac{\theta}{2}=\frac{1-cos\theta}{2}\) Harversine

进一步我们可以得到： \(A = (lat_a, lng_a)\) \(B = (lat_b, lng_b)\) \(N = (\frac{\pi}{2}, 0)\) \(hav(NB) = hav(AB-AN)+sin(AB)sin(AN)hav(\angle NAB)\) 再往下算基本就吐了，这公式长到打在 Wolfram Alpha 上直接不识别。只好上网找了个算好的结果： \(tan(\theta)=\frac{|lng_b-lng_a|}{ln(\frac{tan(\frac{lat_B}{2}+\frac{\pi}{4})}{tan(\frac{lat_A}{2}+\frac{\pi}{4})})}\) 需要特别注意，当 \(lat_a = lat_b\) 的时候分母为 0，针对这类情况，大多数编程语言都有 atan2(y, x) 函数，当 x = 0 时返回 90 度。最后我们有程序：

delta_phi = Math.log(Math.tan((@latitude / 180 * Math::PI) / 2 + Math::PI / 4) / Math.tan((orbit.latitude / 180 * Math::PI) / 2 + Math::PI / 4))
delta_lon =  (@longitude - orbit.longitude)  / 180 * Math::PI
theta = Math.atan2(delta_lon, delta_phi)
target_heading = theta * 180 / Math::PI

偏航控制

飞机上有两个可以控制飞机转向的方法，一个是偏航（Yaw），另一个是组合使用滚转（Roll）和俯仰（Pitch）。偏航通常是通过垂直尾翼来产生偏航力矩。而滚转和俯仰由副翼和水平尾翼得到。显然副翼和水平尾翼比垂直尾翼大很多，控制也会更快速、灵敏。事实上我们只需要控制滚转即可，因为当我们控制滚转，飞机的升力面会减少，从而导致升力下降、飞机下降；为了保持飞行高度，我们基于飞行高度控制的俯仰自然会提高俯仰，从而产生偏航方向的力矩。

不过需要注意两个关键点：

控制俯仰来控制升力的原理是，在一定范围内攻角（Angle of Attack）和升力系数成正比。然而当攻角大于某个角度，升力可能会迅速下降（即失速），如果要提高升力应当降低俯仰，而不是继续抬升俯仰。
当滚转角度越来越大后，副翼的升力面会逐渐减小到无论如何提高节流阀大小或调整俯仰都无法维持的情况（即失速），应当将侧倾角度（bank angle）控制在合理范围内。

在控制程序中我直接限制了俯仰的范围是 [-5.0, 10] 度，而滚转限制在正负 25 度以内。整体程序如下：

class WaypointProcess
  def initialize(vessel, velocity, height, latitude, longitude)
    @vessel = vessel
    @control = vessel.control

    @velocity = velocity
    @height = height
    @longitude = longitude
    @latitude = latitude

    @throttle_controller = PIDController.new(0.1, 0.01, 0.2)
    @pitch_controller = PIDController.new(0.05, 0.05, 0.1, -1.0, 1.0)
    @roll_controller = PIDController.new(0.0005, 0.01, 0.7, -1.0, 1.0)
  end

  def run
    @control.sas = false
    loop do
      orbit = @vessel.flight(@vessel.orbit.body.reference_frame)
      surface = @vessel.flight(@vessel.surface_reference_frame)
      break if (orbit.latitude - @latitude).abs < 1e-4 and (orbit.longitude - @longitude).abs < 1e-4

      throttle = @throttle_controller.trigger(@velocity, orbit.speed)
      @control.throttle = throttle

      pitch = @pitch_controller.trigger(@height, orbit.mean_altitude)
      if pitch > 0.0 and surface.pitch > 10
        pitch = -0.1
      elsif pitch < 0.0 and surface.pitch < -5
        pitch = 0.1
      end
      @control.pitch = pitch

      delta_phi = Math.log(Math.tan((@latitude / 180 * Math::PI) / 2 + Math::PI / 4) / Math.tan((orbit.latitude / 180 * Math::PI) / 2 + Math::PI / 4))
      delta_lon =  (@longitude - orbit.longitude)  / 180 * Math::PI
      theta = Math.atan2(delta_lon, delta_phi)
      target_heading = theta * 180 / Math::PI

      target_heading = 360 + target_heading if target_heading < 0
      delta_heading = target_heading - surface.heading

      delta_heading = 360 - delta_heading if delta_heading > 180
      delta_heading = delta_heading + 360 if delta_heading < -180

      bank_angle = delta_heading
      bank_angle = 25 if delta_heading > 25
      bank_angle = -25 if delta_heading < -25

      roll = @roll_controller.trigger(bank_angle, surface.roll)
      @control.roll = roll
      current_roll = surface.roll
    end

    puts "Waypoint lat: #{@latitude}, lng: #{@longitude} Reached."
  end
end

测试

我们使用如下的飞行路径设定：

require 'matrix'
require 'krpc'

require './libs/controller/pid'
require './libs/process/takeoff'
require './libs/process/waypoint'

KRPC.connect do |client|
  vessel = client.space_center.active_vessel

  # VR: 100m/s, Climb at 390 knots to 2000m
  TakeoffProcess.new(vessel, 100, 200, 2000).run
  # Fly to North pole (N90, S0.0) at 330 knots at FL300
  WaypointProcess.new(vessel, 170, 7000, 90.0, 0.0).run
end

在 100m/s 时抬轮，以 390 节速度爬升到 2000 米，然后爬升到 30000 英尺转向飞往北极点。测试完美。

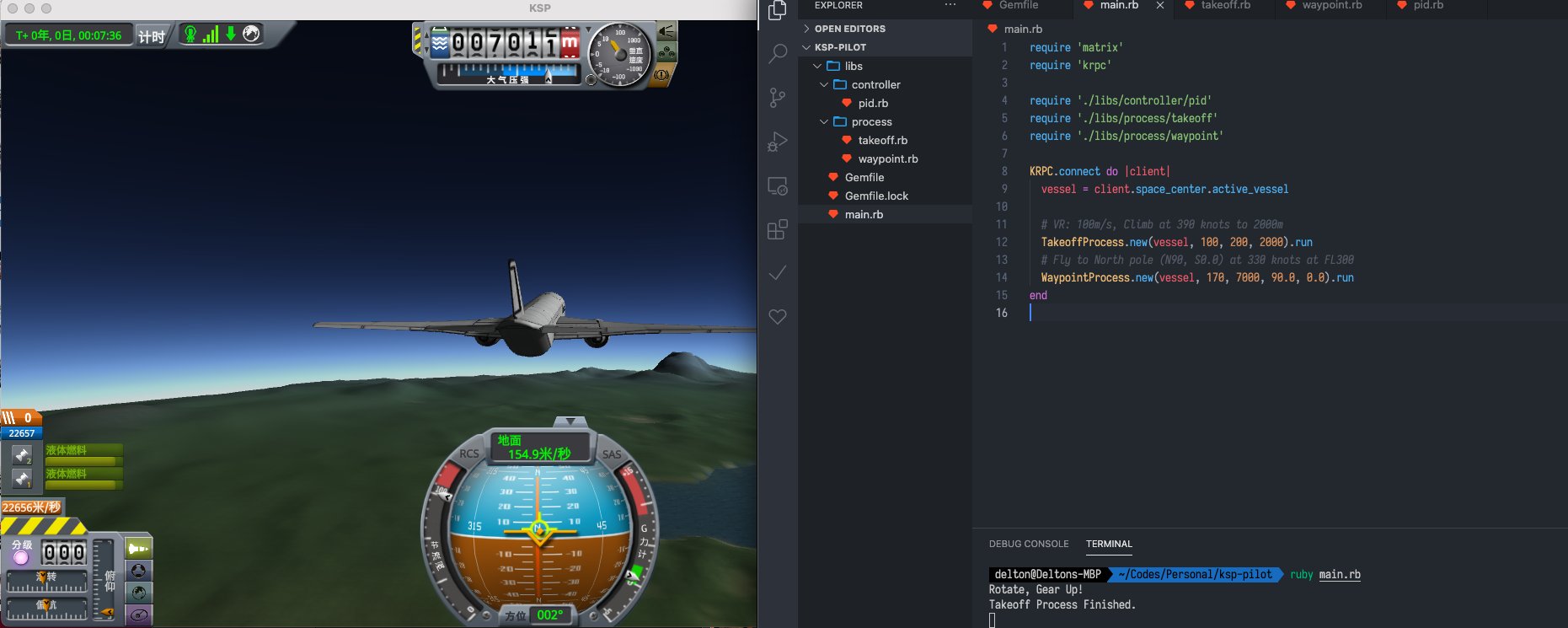
KSP AP Test

完整代码：GitHub dsh0416/ksp-pilot

我用的是自带存档强翼 A300 进行的测试。该飞机被设计成大气层内飞行的重型运输机。由于 Kerbin 星球比起地球大气稀薄，到 FL300 飞机已经难以维持 300 节的时速了。不过如果使用空天飞机进行测试则没有这样的问题。

目前的 PID 曲线的调教比较保守，在高度控制上震荡比较厉害。这可以针对具体飞机进行调整，如果在安装 Ferram Aerospace Research 的情况下，可以获得具体的「升力系数参数」，其实通过控制升力系数来控制高度是最为可靠的方法，现实中的飞机也是这么做的。

之后如果能获取机场 GPS 坐标实现自动进近和降落应该会更有意思。

不过这个项目还是很有意义的，不但练习了 Ruby 编程，还学习了立体几何、物理、飞行原理和自动化控制的相关知识。

CodeRemixer

PID 控制

起飞控制

方向角计算

偏航控制

测试